Teorija verovatnoće i statistika mogu biti jako moćni alati bez kojih su nezamislive pojedine oblasti nauke, ali se takođe mogu koristiti za otkrivanje prevara i tajnih podataka što je ilustrovano kroz tri priče u antrfileima.
Piše dr Milovan Šuvakov
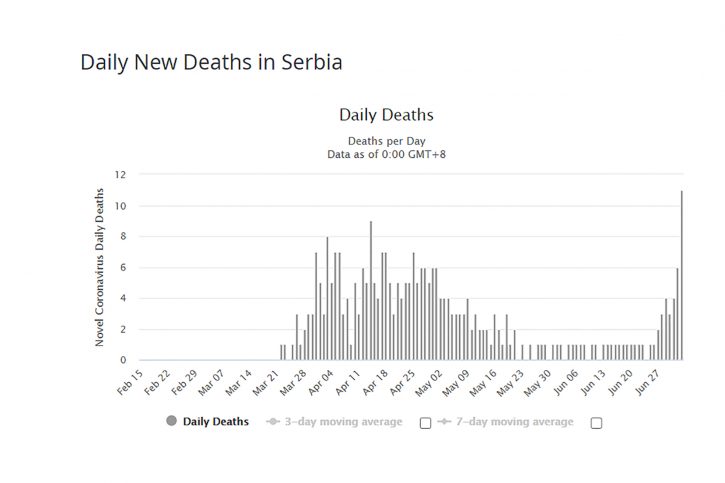
Kolega Igor Smolić je nedavno, koristeći se sličnom matematikom, pokazao da se rezultati o broju zvaničnih smrti od COVID-19 po danu ne poklapaju sa očekivanim distribucijama iz matematičkih modela.
Poređenjem sa podacima iz ostalih zemalja u svetu koje su imala sličan broj prijavljenih smrtnih dogadjaja tokom istog perioda posmatranja pokazali smo da Srbija jedina odstupa. U međuvremenu su se, kako na društvenim mrežama tako i u poslednjem „Utisku nedelje“, otvorila pitanja koliko se ovde može verovati statistici, posebno kada su u pitanju optužbe da neko manipuliše podacima.
Ovim tekstom želim da odgovorim na ova pitanja, da stanem iza tvrdnje da podaci nisu dobri i da na jedan jednostavan način približim čitaocima sa prosečnim znanjem matematike kako je moguće proceniti ovu šansu.
Broj nemačkih tenkova
Tokom Drugog svetskog rada saveznici su morali da imaju dobru procenu obima proizvodnje tenkova od strane Nemačke. U ovaj poduhvat uključile su se obaveštajne službe, ali i matematičari.
Tokom rata kada bi vojnici pronalazili ostatake nemačkih tenkova i drugog oružja, tražili bi serijske brojeve delova koje su potom matematičari koristili da na osnovu njih urade potrebnu procenu obima proizvodnje. Ovaj metod se pokazao mnogo boljim od konvencionalnih obaveštajnih metoda.
Recimo, za avgust 1942. metodom serijskih brojeva je procenjeno da je Nemačka proizvela 327 tenkova, dok su obaveštajni podaci davali procenu od 1550. Posle rata se ispostavilo da je pravi broj 342. Više primera možete naći u radu ili na Vikipediji.
Ako brojite koliko puta dnevno se desi sudar u vašem delu grada, koliko puta godišnje padne veći meteor na Zemlju ili koliko puta u sekundi zapišti Gajgerov brojač ako ste u blizini radioaktivnog izvora, brojevi koje dobijete pratiće tzv. Poasonovu distribuciju.
Kada god u prirodi ili u društvu imamo događaje koji se odvijaju tako da su nezavisni jedan od drugoga i sa konstantnom stopom u vremenu – oni se distribuiraju po toj raspodeli. To konkretno znači da, ako znamo srednji broj događaja u vremenu, tzv. stopu kojom se odvijaju ovi događaji, možemo je uneti u jednu formulu koja pokazuje koliko često možemo očekivati nulu, jedinicu, dvojku, itd.
Možemo da uradimo i obrnuto: koristeći se statističkim metodama na osnovu podataka koje izmerimo možemo da izračunamo kolika je stopa i koliko je izvesno da podaci prate ovu raspodelu.
Broj smrtnih slučajeva od COVID-19 su upravo jedan ovakav proces u intervalima kada je stopa konstantna. Nezavisnost je obezbeđena pošto u standardnim okolnostima smrt jednog pacijenta ne može da utiče na to da li će i kada da umre neki drugi pacijent.
Ovaj uslov nije zadovoljen samo u ekstremnim slučajevima – kada pacijenti zauzimaju resurse koji mogu značiti drugima, npr. respiratore. Tada smrt jednog pacijenta može imati uticaj na drugog. I tada je teško da ova zavisnost bude jaka na vremenskim skalama od jednog dana.
Međutim, ako posmatramo period od mesec dana kada su zvanični podaci prikazivali pojedinačne slučajeve sa različitih krajeva zemlje, u momentima kada respiratori i drugi resursi nisu bili ni blizu popunjeni, pojedinačni smrtni ishodi moraju biti nezavisni jedni od drugih.
Kolega Smolić je pretpostavio da je u intervalu koji je posmatrao od 21 dana sa 18 smrtnih slučajeva stopa bila konstantna i uz pomoć statističkih testova (Kolmogorov-Smirnovljev i hi-kvadrat) sračunao da je verovatnoća da zvanični podaci ne odstupaju od očekivane Poasonove distribucije značajno manja od 1%, što odgovara kvoti u kladionici manjoj od 1.01. Ovo je dovoljno da probudi ozbiljnu sumnju u verodostojnost podataka.
Of all the countries in the world, Serbia has the most unique Covid worldometer graph. Can you guess, based on this graph, when did the election campaign in Serbia take place? You only get one try. pic.twitter.com/mq0BA9pGdj
— Viktor Marković (@Belgrade) July 3, 2020
Jedan deo kritika upućenih na ovu analizu odnosio se na pretpostavku da je stopa konstantna. Bez obzira što je Igor ponovio test na kraćim intervalima od sedam dana, što je dovoljno kratko da se ne očekuje značajna promena, i dobio sličan rezultat, formalno mi zaista na prvi pogled ne znamo da li je došlo do brzih promena stope koji bi narušili pretpostavku.

Dve činjenice ovde opravdavaju korišćenje ovog metoda. Prva je da se kod ovog procesa očekuje da je promena stope mala kada je sama stopa mala. Stopa je tokom ovog perioda manja od jedan pošto bi u suprotnom očekivali mnogo većih brojeva u podacima. Zato očekujemo da je i promena stope mala.
Druga činjenica se odnosi na potpuno različit trend koji vidimo kod podataka (slika 1a) i u očekivanoj raspodeli koja je opadajuća (slika 1b). Drugim rečima dominantan uticaj na rezultat testa imaće ovaj obrnut odnos broja jedinica i nula, a ne precizna vrednost stope.
U slučaju kada je stopa znatno veća, distribucija je daleko od onoga što vidimo (slika 1c) te taj slučaj možemo isključiti.

Sjajna stvar je što ne moramo da se zadržimo na teoriji, pošto ovo možemo da simuliramo i vidimo šta se dešava kada menjamo stopu. Ako kliknete na ovaj link otvoriće vam se interaktivni aplet koji je zapravo računarska simulacija jednog ovakvog procesa. Pokušajte da se igrate i menjate stope događaja pomerajući „regler“.
Videćete da koliko god se igrali, ne možete ni blizu dobiti raspodelu u kojoj imate mnogo više jedinica nego nula, a da nemate nijedan broj veći od 1. Ono što ćete dobijati ukoliko ne preterate sa reglerom, ličiće na distribucije iz drugih zemalja koje su prikazane na slici 2.

Ovde prikazujemo malo širi vremenski period od 30 dana kada smo imali 25 smrtna slučaja. Na grafikonima su 28 država koje su u tih 30 dana imale više od 10, a manje od 40 preminulih. Grafikon predstavlja koliko od 30 dana ima sa 0, 1, 2, 3 ili 4 umrlih. Distribucija je znatno dugačija u našem slučaju kao jedinom gde je broj dana sa jednim smrtnim slučajem znatno veći od broja dana bez preminulih (nula), a uz to nema dana sa više od jednog preminulog.
I bez statističkih testova, poređenje sa drugim državama jasno pokazuje da je u slučaju naših podataka nešto naopako. Ali hajde da se ne zadržimo tu.
U ovom slučaju se zaista radi o malim brojevima kako je to u „Utisku nedelje“ pomenuo dr Srđa Janković i, da budemo precizniji, radi se o dva najmanja nenegativna cela broja, 0 i 1. Imajući ovo u vidu, stvari postaju jednostavnije, te verovatnoću da dođe do ovakvog niza događaja bez većih brojeva od jedan možemo direktno izračunati iz teorije verovatnoće – bez korišćenja ikakvih standardnih testova.
Ovako ćemo dobiti bolju procenu, pošto su testovi pravljeni za generalnije primene i mogu da precene u pojedinim konkretnim slučajevima poput ovoga.
Ako pretpostavimo da je svaki momenat smrti potpuno nezavisan, odnosno da se nezavisno jedan od drugoga desio slučajno izabranog dana, dobijemo da je šansa da se ni u jednom danu nisu desila dva smrtna slučaja 1 prema skoro 4 miliona (preciznije 1:3.833.121).
Koga zanimaju matematički detalji kako se ovo može izračunati, neka pogleda sledeći antrfile. Šta ovaj rezultat znači? Kao što je prof. Zoran Radovanović rekao, kada bi se ova epidemija ponovila četiri miliona puta, samo jednom bismo očekivali ovakvu raspodelu.
Računanje verovatnoće – model 1
U ovom modelu događaji su potpuno nezavisni sa ravnomernom šansom da se svaki desi od prvog do tridesetog dana. Ovo se svodi na takozvani problem istog rođendana, koji je poznat po činjenici da je šansa preko 50% da među 23 osobe koje su slučajno skupile postoje dve sa istim datumom rođenja.
Modifikacija je što ovde umesto 365 dana u godini imamo 30 dana od kojih su slučajno izabrana 25. Šansa da se ni jedan dan ne izabere dva puta, što odgovara onome što podaci pokazuju, računa se na sledeći način:
Izbor prvog dana je proizvoljan. Kada je prvi dan “izabran” šansa da se drugi ne poklopi sa tim danom je 29/30 pošto su 29 dana od 30 bez događaja, za sledeći da se ne poklopi sa prethodna dva izabrana 28/30, …, na kraju za dvadeset i peti događaj je 6/30. Verovatnoća da se svi ovi događaji sukcesivno dese na ovaj način je proizvod ovih brojeva odnosno 1/3833121.1 = 0.00000027.
Pošto ne želim da ostavim prostora za sumnju ni u pretpostavku nezavisnosti događaja, izneću model koji ima za cilj da proceni maksimalnu šansu da se ovo desi slučajno čak i kada su događaji zavisni uz minimalnu stohastiku od jednog dana.
To znači da je u ovom modelu svaka smrt vremenski predodređena, samo je pitanje da li se dešava tog dana ili sutradan. I pored ovoliko veštačkog natezanja da povećamo šanse da podaci nisu lažirani, dobijemo šansu od jedan u milion. U sledećem antrfileu imate detalje računa.
Računanje verovatnoće – model 2
U ovom modelu svaki događaj se može desiti samo u dva predodređena sukcesivna dana, raspoređena redom tako da svaki počinje u momentu kada u podacima imamo događaj. Na ovaj način imamo četiri mesta u ovih 30 dana kada se ne preklapaju ovi intervali, odnosno pet podgrupa jedinica koje su uzastopne.
Ako pogledamo grupu jedinica dužine m, šansa da se događaji ne poklope je 2/2^m pošto od svih kombinacija samo dve nemaju preklapanje (kada su se smrti u svih m slučajeva desile na prvi dan, ili kada su se sve desile sutradan).
Ako izmnožimo ove šanse za svih pet grupa sukscesivnih jedinica dobićemo 2^5/2^25 odnosno 1:2^20 (1048576).
Po ovoj analizi podaci nisu samo netačni već su najverovatnije rukom modifikovani. Da je korišćena bilo kakva konzistentna metodologija koja, na primer, ne bi brojala sve, već samo neku podgrupu pacijenata, raspodela bi i dalje morala da prati Poasonovu raspodelu.
Do podataka koje vidimo dolazi samo ako se veštački na kraju brojevi spuštaju ili podižu na jedan. Uz pretpostavku da su brojevi samo spuštani na jedan, poput karikature sa Tvitera, na osnovu broja nula možemo da procenimo da je prava stopa umiranja bila oko 1.8 na dnevnom nivou, odnosno da je broj smrti u podacima pre „trimovanja“ tokom ovih mesec dana bio veći za oko 30 preminulih.
— Kablo Eskobar (@storm_triper) June 28, 2020
O autoru
Autor je istraživač koji je dobar deo karijere proveo modelujući i analizirajući procese poput ovog u raznim oblastima nauke, od fizike plazme, preko nanostruktura i društvenih mreža do bioinformatike.
Benfordov zakon
Ako otvorite novine ili veb sajt iz bilo koje oblasti i naletite na neki broj, šansa da on počinje sa brojem jedan je skoro trećina, dok se broj devet kao vodeća cifra javlja mnogo ređe, svega jednom u dvadeset brojeva. Ovo se odnosi na skoro sve brojeve koju potiču iz realnog života, suprotno intuiciji.
Šanse za prve cifre nisu iste. Te šanse zapravo prate specifičnu raspodelu u kojoj se cifra 1 pojavljuje u 30.1% slučajeva, veće cifre se pojavljuju na prvom mestu sa sve manjom šansom, sve do cifre 9 koja se pojavljuje 4.6%. Ovo mogu biti bilo kakvi brojevi koji potiču iz prirode ili društva, npr. rezultati merenja, brojevi koji se pojavljuju u finansijskim dokumentima, rezultati izbora, itd.
Međutim, kada ljudi izmišljaju brojeve iz glave, npr. manipulišu njima, oni ne prate ovu raspodelu. Zato se Benfordov zakon koristi često u forenzici za otkrivanje prevara, a u nekim zemljama se može koristi i na sudu.
Zvanični podaci koje države objavljuju u raznim oblastima se često testiraju na ovaj način. Na primer, u poslednjih par meseci je izašlo više radova u kojima se testiraju zvanični podaci o covid-19 pandemiji. Podatke iz naše zemlje na ovaj način za sada nije moguće testirati, jer je neophodna veća statistika pa se do sada ova vrsta analize primenila na proveru verodostojnosti podataka iz Kine, kao i na zemlje poput SAD i Italije.
Legenda o Poenkareu i pekari
Postoji legenda o čuvenom francuskom matematičaru Henriju Poenkareu i pekari u kojoj je svaki dan kupovao hleb. Nakon godinu dana tužio je pekara zbog prevare pošto tvrdi da prodaje hleb od 1kg, a njegova statistika kupljenih hlebova ima srednju vrednost 950 grama.
Sledeće godine Poenkare je nastavio da dolazi, a pekar mu je uvek davao neku od većih vekni kako bi izbegao tužbu. Na kraju godine Poenkare ga je optužio da vara druge ljude bez obzira što je prosek onih hlebova koje je on kupio bio 1 kg.
Kako je znao? Tako što je distribucija odstupala od one koja treba da bude. Umesto tzv. normalne distribucije koja je simetrična dobio je rep te distribucije. Na osnovu toga je mogao čak i da izračuna prosečnu težinu onih hlebova koje nikada nije kupio niti merio.
Pratite nas i na društvenim mrežama:
Učestvuj u diskusiji ili pročitaj komentare